Modeling the Conformational Preference of the Lignocellulose Interface and Its Interaction with Weak Acids
I am happy to anounce a new publication which I worked on alongside Bun Chan and Takahito Nakajima available in the Journal of Physical Chemistry A. This paper is a study of various conformers of model systems of lignin. The conformers were generated by a thorough screening process which went all the way from forcefields down to an approximation for CCSD(T)/CBS. I think studies like this can be performed for many different types of systems so I hope our detailed description of the screening procedure is of use especially to novices in the field.
One of the tools I found very useful when we did our study is OpenBabel. Many people think of OpenBabel as just a tool for converting molecular file formats, but is is so much more. The best way to see this is to look at the Developer Documentation. All of these classes can be accessed by your own driver program. And since they use Swig, they can be accessed not just from C++ but also from Python.
istr = """24
O 0.47000 2.56880 0.00060
O -3.12710 -0.44360 -0.00030
N -0.96860 -1.31250 0.00000
N 2.21820 0.14120 -0.00030
N -1.34770 1.07970 -0.00010
N 1.41190 -1.93720 0.00020
C 0.85790 0.25920 -0.00080
C 0.38970 -1.02640 -0.00040
C 0.03070 1.42200 -0.00060
C -1.90610 -0.24950 -0.00040
C 2.50320 -1.19980 0.00030
C -1.42760 -2.69600 0.00080
C 3.19260 1.20610 0.00030
C -2.29690 2.18810 0.00070
H 3.51630 -1.57870 0.00080
H -1.04510 -3.19730 -0.89370
H -2.51860 -2.75960 0.00110
H -1.04470 -3.19630 0.89570
H 4.19920 0.78010 0.00020
H 3.04680 1.80920 -0.89920
H 3.04660 1.80830 0.90040
H -1.80870 3.16510 -0.00030
H -2.93220 2.10270 0.88810
H -2.93460 2.10210 -0.88490
"""
from openbabel.openbabel import OBMol, OBConversion
conv = OBConversion()
mol = OBMol()
conv.SetInFormat("xyz")
conv.ReadString(mol, istr)
Iterators are exposed as their own special classes.
from openbabel.openbabel import OBMolAtomIter
for at in OBMolAtomIter(mol):
print(at.GetAtomicMass(), at.GetX(), at.GetY(), at.GetZ())
15.9994 0.47 2.5688 0.0006
15.9994 -3.1271 -0.4436 -0.0003
14.0067 -0.9686 -1.3125 0.0
14.0067 2.2182 0.1412 -0.0003
14.0067 -1.3477 1.0797 -0.0001
14.0067 1.4119 -1.9372 0.0002
12.0107 0.8579 0.2592 -0.0008
12.0107 0.3897 -1.0264 -0.0004
12.0107 0.0307 1.422 -0.0006
12.0107 -1.9061 -0.2495 -0.0004
12.0107 2.5032 -1.1998 0.0003
12.0107 -1.4276 -2.696 0.0008
12.0107 3.1926 1.2061 0.0003
12.0107 -2.2969 2.1881 0.0007
1.00794 3.5163 -1.5787 0.0008
1.00794 -1.0451 -3.1973 -0.8937
1.00794 -2.5186 -2.7596 0.0011
1.00794 -1.0447 -3.1963 0.8957
1.00794 4.1992 0.7801 0.0002
1.00794 3.0468 1.8092 -0.8992
1.00794 3.0466 1.8083 0.9004
1.00794 -1.8087 3.1651 -0.0003
1.00794 -2.9322 2.1027 0.8881
1.00794 -2.9346 2.1021 -0.8849
OpenBabel will give you access to some forcefields, so you can do things like geometry optimization.
from openbabel.openbabel import OBForceField
opt_mol = OBMol(mol)
ff = OBForceField.FindForceField("mmff94")
ff.Setup(mol)
ff.SteepestDescent(1000, 1e-5)
ff.GetCoordinates(opt_mol)
print(ff.Energy(), ff.GetUnit())
-122.52811655381508 kcal/mol
And it has some useful routines for aligning molecules, for when you're trying to screen out duplicates.
from openbabel.openbabel import OBAlign
align = OBAlign()
align.SetRefMol(mol)
align.SetTargetMol(opt_mol)
align.Align()
print(align.GetRMSD())
0.02329795381669716
One other thing we can do with openbabel is a conformer search. Let's start with a smiles rep.
istr = """C(C(C(=O)O)N)S"""
conv = OBConversion()
mol = OBMol()
conv.SetInFormat("can")
conv.ReadString(mol, istr)
mol.AddHydrogens()
Generate a 3D representation.
from openbabel.openbabel import OBBuilder
builder = OBBuilder()
builder.Build(mol)
Now do the search.
from openbabel.openbabel import OBConformerSearch
conf = OBConformerSearch()
conf.Setup(mol)
conf.Search()
conf.GetConformers(mol)
print(mol.NumConformers())
30
Let's rescore the conformers with a forcefield and optimize.
ff = OBForceField.FindForceField("gaff")
energies = []
opt_energies = []
for i in range(mol.NumConformers()):
mol.SetConformer(i)
ff.Setup(mol)
energies.append(ff.Energy())
ff.SteepestDescent(10000, 1e-5)
ff.GetCoordinates(mol)
opt_energies.append(ff.Energy())
from matplotlib import pyplot as plt
fig, axs = plt.subplots(1, 1)
axs.plot(energies, 'kx', markersize=12, label="Conformer Energy")
axs.plot(opt_energies, 'r+', markersize=12, label="Optimized Energy")
axs.set_ylabel("Energy (" + ff.GetUnit() + ")", fontsize=14)
axs.set_xlabel("Conformer ID", fontsize=14)
axs.legend(bbox_to_anchor=(1, 1))
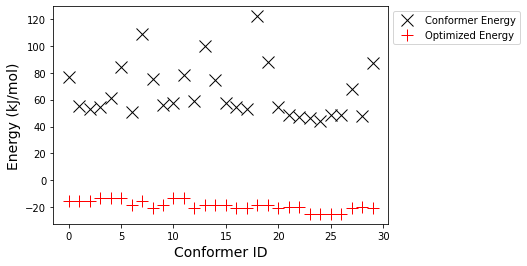
Interestingly, we notice that there are a number of conformers with very similar energy values after optimization. Of course the goal of the conformer search is to identify a diverse set of possible structures, and optimization can destroy that diversity. Let's verify if that's what happened by looking at the RMSD between optimized structures.
from numpy import zeros
mat = zeros((mol.NumConformers(), mol.NumConformers()))
align = OBAlign()
for i in range(mol.NumConformers()):
mol.SetConformer(i)
align.SetRefMol(mol)
for j in range(mol.NumConformers()):
mol.SetConformer(j)
align.SetTargetMol(mol)
align.Align()
mat[i, j] = align.GetRMSD()
fig, axs = plt.subplots(1, 1)
img = axs.imshow(mat, cmap="Greys", aspect="auto")
cb = fig.colorbar(img)
cb.set_label("RMSD", fontsize=14)

That's a lot of white. So let's try removing the duplicates.
duplicates = []
for i in range(mol.NumConformers()):
for j in range(i+1, mol.NumConformers()):
if mat[i,j] < 1e-1:
duplicates.append(j)
duplicates = sorted(set(duplicates), reverse=True)
for idx in duplicates:
mol.DeleteConformer(idx)
print(mol.NumConformers())
8
We've made it this far, so let's finish with a higher level energy estimate using PySCF and density functional theory.
from pyscf.gto import Mole
pmols = []
for i in range(mol.NumConformers()):
mol.SetConformer(i)
atlist = []
for at in OBMolAtomIter(mol):
atlist.append(str(at.GetAtomicNum()) + " " +
str(at.GetX()) + " " +
str(at.GetY()) + " " +
str(at.GetZ()))
pmols += [Mole(atom=";".join(atlist), basis="6-31G*")]
pmols[-1].build()
from pyscf import dft
dft_energy = []
for m in pmols:
rks = dft.RKS(m)
rks.xc = "B3LYP"
rks.verbose = False
dft_energy += [rks.kernel()]
ff_energy = []
for i in range(mol.NumConformers()):
mol.SetConformer(i)
ff.Setup(mol)
ff_energy.append(ff.Energy())
fig, axs = plt.subplots(1, 1)
axs.plot([x - min(ff_energy) for x in ff_energy],
[(x - min(dft_energy))*2600 for x in dft_energy], 'kx', markersize=14)
axs.ticklabel_format(useOffset=False)
axs.set_xlabel("(Relative) Forcefield Energy (" + ff.GetUnit() + ")", fontsize=14)
axs.set_ylabel("(Realtive) DFT Energy (kJ/mol)", fontsize=14)

Of course, no screeing procedure should end at B3LYP/6-31G*! But I hope this post has shown to you that OpenBabel can serve as a useful toolkit for building your next study.